Evaluation

To estimate the performance of a recommender system, evaluation is needed. Gorse provides both online evaluation and offline evaluation.

Online Evaluation

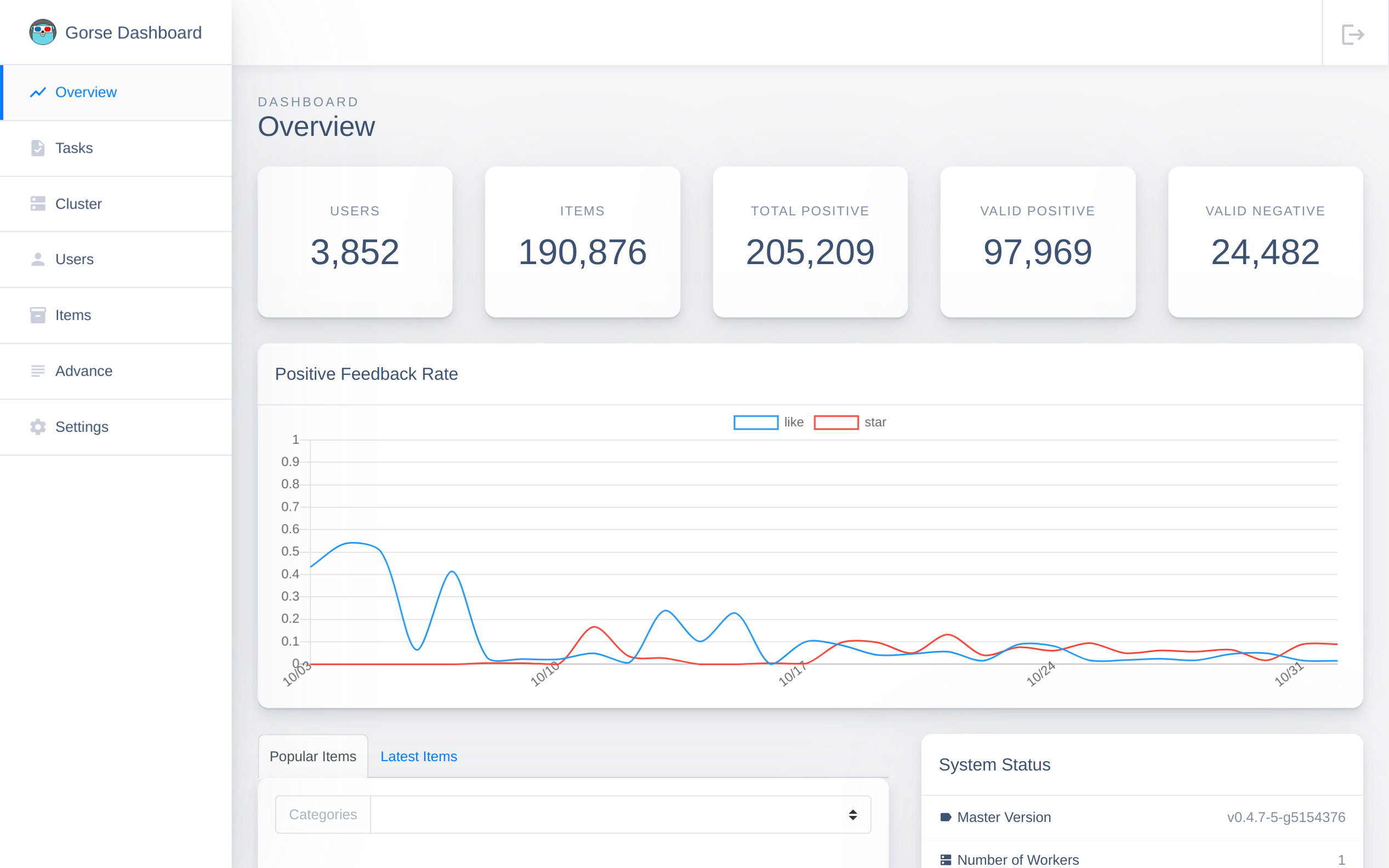
The target of a recommender system is to maximize the probability every user like recommended items. Thus, the metric for online evaluation is the positive feedback rate

$$\text{positive rate}=\frac{1}{|U|}\sum_{i\in |U|}\frac{|R^p_u|}{|R^r_u|}$$

where $R^r_u$ is the set of read feedback from user $u$, and $R^p_U$ is the set of a specific positive feedback. Gorse calculates positive rates every day and plots them as the line chart.

For example, there are two positive feedback types (like and star) in GitRec. Thus, the like rate and star rate are shown on the overview page of the dashboard.

Offline Evaluation

Offline evaluation is used to estimate the performance of an individual algorithm. It allows users to inspect the status of an individual algorithm. Thus, this section is organized by different algorithms.

Factorization Machine

The factorization machines model predicts the probability that a user gives positive feedbacks on an item. Items with top probabilities are recommended to the user. The evaluation algorithm estimates the quality of prediction on given pairs of users and items. The dataset will be divided into a training dataset and a testing dataset. The following metrics will be calculated on the testing dataset.

$$\text{precision}=\frac{tp}{tp+fp}$$

where $tp=|\{i|y_i=1\wedge\hat y_i=1\}|$ and $fp=|\{i|y_i=0\wedge \hat y_i=1\}|$.

$$\text{recall}=\frac{tp}{tp+fn}$$

where $fn=\{i|y_i=1\wedge \hat y_i=0\}$.

$$\text{AUC}=\sum_{i\in P}\sum_{j \in N}\frac{\mathbb{I}(\hat y_i>\hat y_j)}{|P||N|}$$

where $P=\{i|y_i=1\}$ and $N=\{i|y_i=0\}$.

Matrix Factorization

The matrix factorization filters out positive feedback from negative feedbacks and unobserved feedbacks. For each user, Gorse randomly leaves one feedback out of other positive feedbacks as the test item. The matrix factorization model is expected to rank the test item before other unobserved items. Since it is too time-consuming to rank all items for every user during evaluation, Gorse followed the common strategy^[1] that randomly samples 100 items that are not interacted with the user, ranking the test item among the 100 items.

The matrix factorization is evaluated in top 10 recommendations. Suppose the matrix factorization recommends 10 items $\hat I^{(10)}_u$ to user $u$ and the test item is $i_u$

$$\text{HR@10}=\sum_{u\in U}\frac{\mathbb{I}(i_u \in \hat I^{(10)}_u)}{|U|}$$

$$\text{NDCG@10}=\sum_{u \in U}\sum_{i=1}^{10}\frac{\mathbb{I}(i=\hat I^{(10)}_{u,i})}{\log_2(i+1)}$$

where $\mathbb{I}(i=\hat I^{(10)}_{u,i})$ is the $i$-th item in the top 10 recommendations.

Clustering Index and HNSW Index

The clustering index is used to speed up searching user (item) neighbors, while the HNSW index is used to accelerate recommendations from matrix factorization. The quality of an index is evaluated by the recall:

$$\text{recall@n}=\frac{|\text{top n by index}|}{|\text{top n by brute force}|}$$

Tips

The recalls of indices are listed in the "System Status" section of the dashboard homepage.

If the recall of an index is extremely low, consider turning off the index.

---

1. He, Xiangnan, et al. "Neural collaborative filtering." Proceedings of the 26th international conference on world wide web. 2017. ↩︎